Schmoyer Sunquest Sundial
by Robert L. Kellogg
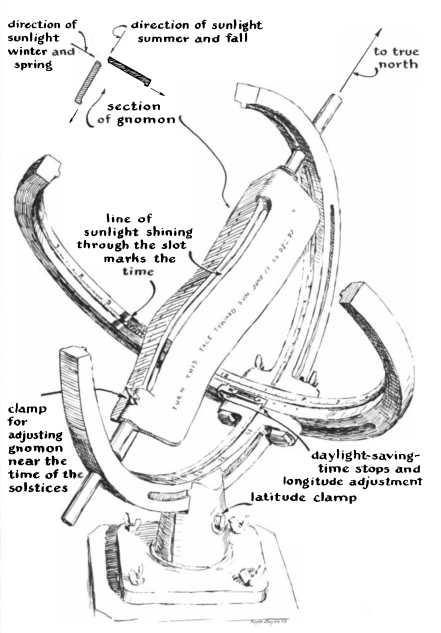 My first encounter with the Schmoyer SUNQUEST Dial occurred many years ago in my youth. I had received an Edmund Scientific 4-inch reflecting telescope with a motorized clock drive for Christmas. By age 14, I wanted to take my telescope to the nearby San Gabriel mountains, so I was delighted by C.L. Strong's Amateur Scientist article in the October 1959 issue of Scientific American describing a transistorized drive for a telescope. But in that October 1959 Amateur Scientist there was also a discussion of a sundial that keeps accurate civil time. I didn’t understand the peculiar gnomon or the shape of the analemma, but somehow this sundial captured my attention.
My first encounter with the Schmoyer SUNQUEST Dial occurred many years ago in my youth. I had received an Edmund Scientific 4-inch reflecting telescope with a motorized clock drive for Christmas. By age 14, I wanted to take my telescope to the nearby San Gabriel mountains, so I was delighted by C.L. Strong's Amateur Scientist article in the October 1959 issue of Scientific American describing a transistorized drive for a telescope. But in that October 1959 Amateur Scientist there was also a discussion of a sundial that keeps accurate civil time. I didn’t understand the peculiar gnomon or the shape of the analemma, but somehow this sundial captured my attention.
In that Amateur Scientist article C.L. Strong quotes a letter from Richard Schmoyer that still holds true today:
"...you raise the question of why a man who owns a accurate watch and several clocks will go to the trouble of building a sundial. Few will disagree with your conclusion that he is motivated in part by the intellectual charm of a device which, without moving parts, can convert the sun's changing position directly into time. But sundial-making holds other attractions for its enthusiasts. In the course of developing a sundial one is exposed to a fascinating and well-defined mixture of mathematics, geometry, geography and astronomy. The design of a sundial challenges our creative talents, and its construction puts our craftsmanship to an exacting test. Finally, the designer who permits the primary time-telling function of the sundial to control its form adds spice to the project. Hardware in pleasing though strange and unexpected shapes often emerges from the equations which describe the ever-changing slant of the sun's rays."
"These inducements led me to design a sundial last year which has become a continuing source of pleasure both to me and to my neighbors. With only a few simple settings during two seasons of the year the sundial can be made to indicate accurate clock time... Most people find sundials attractive, so one must not altogether dismiss their ornamental properties. The structure of my dial was derived from the armillary [sundial]... The transformation from armillary to nested crescents demonstrates how a pleasing shape can emerge from a functional necessity. A good time-telling device should always fulfill its mission."

 There are a number of Schmoyer Sunquest dials in botanical gardens, science museums, and on observatory front lawns. The Sunquest Sundial website describes the man behind the sundial as, "He was a charter member of the North American Sundial Society (member #53) and a member of the British Sundial Society, and was always eager to help aspiring sundialists with their work." The Schmoyer SUNQUEST dial is basically an equatorial sundial of elegant proportions.
There are a number of Schmoyer Sunquest dials in botanical gardens, science museums, and on observatory front lawns. The Sunquest Sundial website describes the man behind the sundial as, "He was a charter member of the North American Sundial Society (member #53) and a member of the British Sundial Society, and was always eager to help aspiring sundialists with their work." The Schmoyer SUNQUEST dial is basically an equatorial sundial of elegant proportions.
Richard Schmoyer, Jr. and Amy Roe, his grand daughter, have created a website in his honor at http://sunquestsundial.org/ . His dials and drawings are posted there for sundial enthusiasts everywhere.
A model of this sundial can be yours. As described below, NASS now 3D prints this unique sundial in PLA plastic.
Go to: NASS Shop - Sundials & Astrolabes
All requests will be filled in the order in which payment is received. If you want a dial for the Southern hemisphere or the original "classic" Schmoyer Sunquest dial without adjustment knob, you must let us know at the time you order the dial.
