By Robert L. Kellogg, Ph. D.

Benjamin Banneker, 1731-1806 , is one of the nation's best-known African American inventors. He was born in Maryland and in 1791 played an important part in surveying the newly designed Federal Territory, now called the District of Columbia. In his youth, Banneker was inspired to build his own clock after an acquaintance gave him a watch. He took the watch apart to find out how it worked and made drawings of each component, and based on his drawings, he carved larger versions of the components out of wood and constructed a clock that kept accurate time for more than 50 years. As mathematician, he designed an Almanac that was a rival of Benjamin Franklin’s famous publication.
As astronomer, clockmaker, and mathematician, he was expected to know how to design sundials, although none exist bearing his mark. In an age before pocket calculators, how would Banneker design a sundial? The graphical method is available in modern texts such as Waugh’s 1973 classic “Sundials: Theory and Construction”. Want to lay out a horizontal sundial without sines, cosines, and tangents? Then this “Sundials for Starters” is for you.
Step 1. On a large drawing paper draw two perpendicular lines. Where they intersect is point “O”, the origin. Somewhere “south” on the vertical line mark a point that we’ll call “S”. From S, draw a slant line that is angled away from vertical by an angle L corresponding to your latitude. To do this, you’ll need a protractor. We’re going to lay out a triangle with this new line such that S,P,O form a right triangle with O-S as the hypotenuse and sides S-P and P-O that meet at right angles. The result should look like Figure 1.
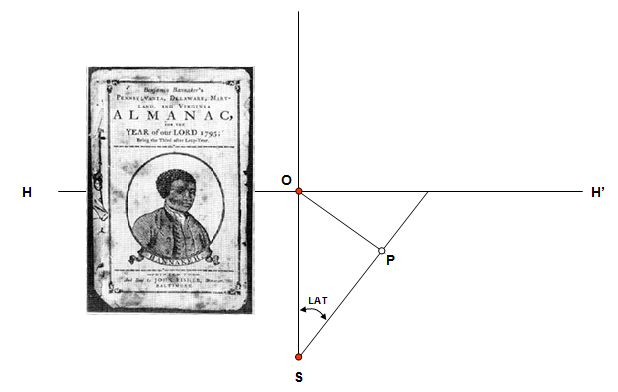
Step 2. Use a compass and draw an circle of radius O-P centered at O. We'll call this “Circle #1” as shown in the figure below. 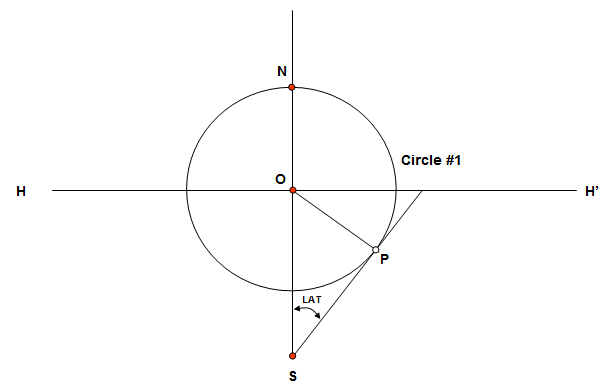
Step 3: Where Circle #1 crosses the vertical line, mark the point as “N” and draw another circle of the same radius around N. We'll call this “Circle #2”. Where the two circles intersect, mark points “A” and "A'". The result should now look like the figure below. The points A, O, and A' are 60 degrees apart as measured from the center N of Circle #2.
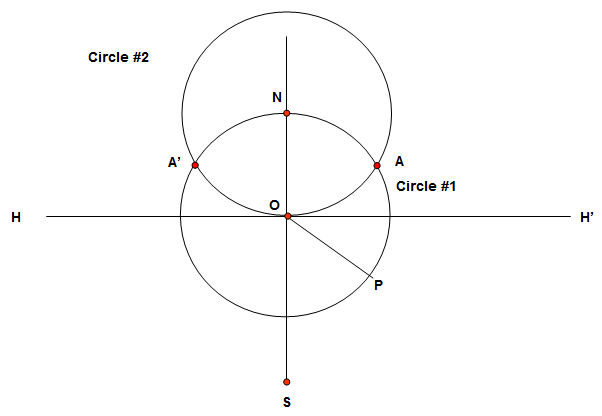
Step 4: We now need to divide the arc O-A into two equal parts, bisecting the points and the angles they represent. Using point A as the center, draw an arc of the same radius as Circle #2. It should pass through point O and through point N, continuing outside of the Circle #2. Use the intersection of this arc and Circle #1 to form a bisecting point, N'. Draw a line N-N' as shown below. The bisecting line does not necessarily pass through point P, and for clarity the lines S-P and P-O have been dropped. Where the line N-N' passes through the circumference of Circle #2, mark point B. We now have points O, B and A on the circumference of Circle #2. These three points are 30 degrees apart as measured from the center N of Circle #2.
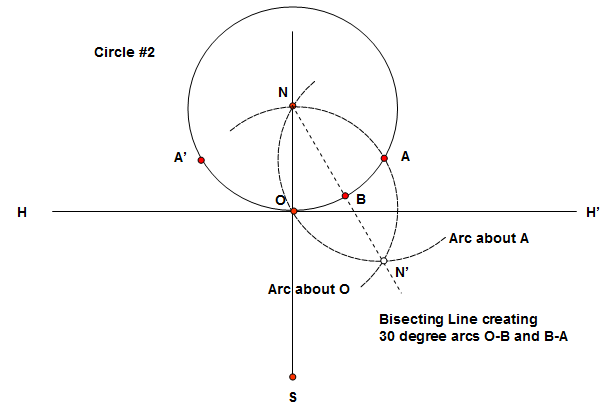
Step 5: Next we repeat this bisecting procerdure on the other side of Circle #1. Using Circle #1 centered on O and an arc about the point B', bisect the arc O-A', using the procedure as above, the mirror image tcreates a point B'. Along the circumference the arcs A'-B', B'-O, O-B, and B-A are spaced 30 degrees apart as measured from the center N of Circle #2.
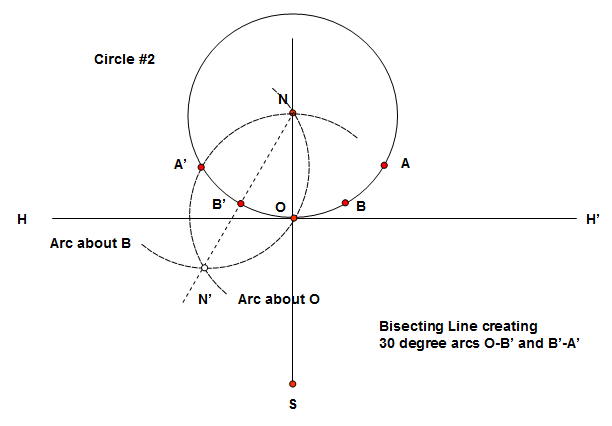
Step 6: We need to further bisect the distance between O and B. Keeping the compass as the radius of Circle #2 (distance O-N) we'll draw two new arcs. One is centered about the point A, going through N of Circle #2 and one is centered about the point B', also going through N of Circle #2. These to arcs intersect at point N and at a point outside the circle N". Draw a line between N-N' and as before, where this line crosses the circumference of Circle #2, mark a point we'll call E. The distances O-E and E-B on the circumference are now 15 degrees of arc as measured from the center N of Circle #2.
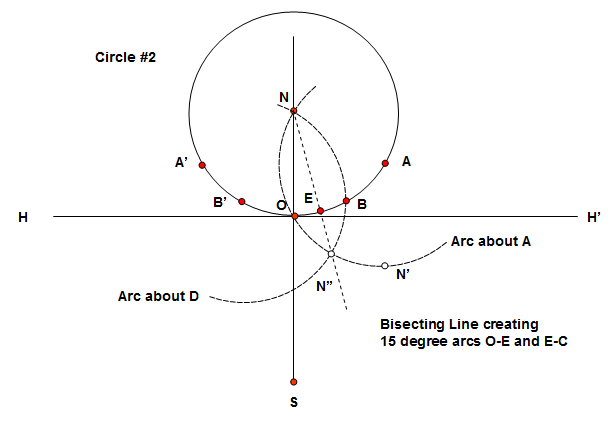
Step 7: We could do a mirror image of the above figure, but instead, readjust the compass to the distance O-E. Now from B measure and mark point F and in similar manner from A measure and mark point G. On the other side of the circle, measure from O and mark E' and in similar manner from B' mark F' and from A' mark G' all on the circumference of Circle #2
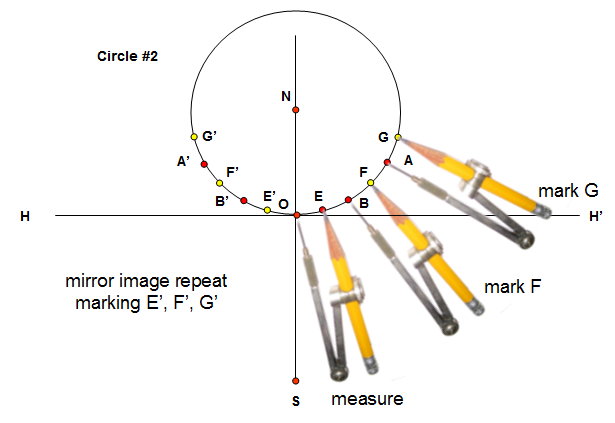
Step 8: From N draw lines through each of the circumference points of Circle #2 to the horizontal line H-H’. Where the extended lines (auxillary hour lines) intersect the line H-H', mark the points as shown in the figure bellow:
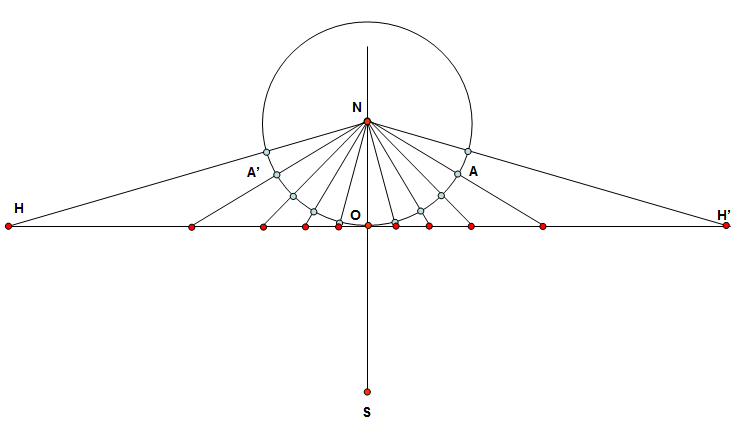
Step 9: Continue drawing lines from the points on H-H' down to the starting point S as done in the next figure. From left to right we have the sundial hour lines from 7am to 5pm. Draw a horizontal line through S that is parallel to H-H'. This will be the 6am and 6pm line.
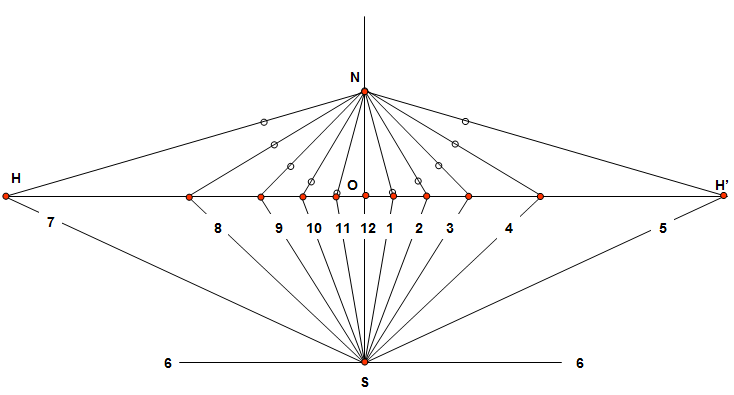
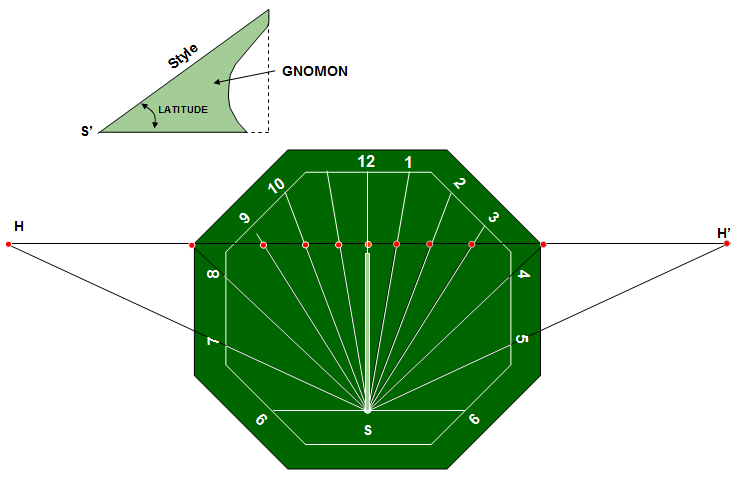
Step 10: We now have all the sundial hour lines from 6am to 6pm centered on point S. With a little bit of clean-up, the radiating hour lines can be trimmed to form a sundial. In the figure below the dial plate is made part of a circle, but it could be designed using a squre or octagonal design. This is where art takes over the science of drawing the sundial. And that initial right triangle that was formed in Step 1? It can now be used to form the gnomon, the dial’s shadow caster. The triangle stands upright, perpendicular to the dial plate that we’ve just designed. Its pointy end S’ is placed on the dial plate at S, with the rest of the gnomon following the noon line.
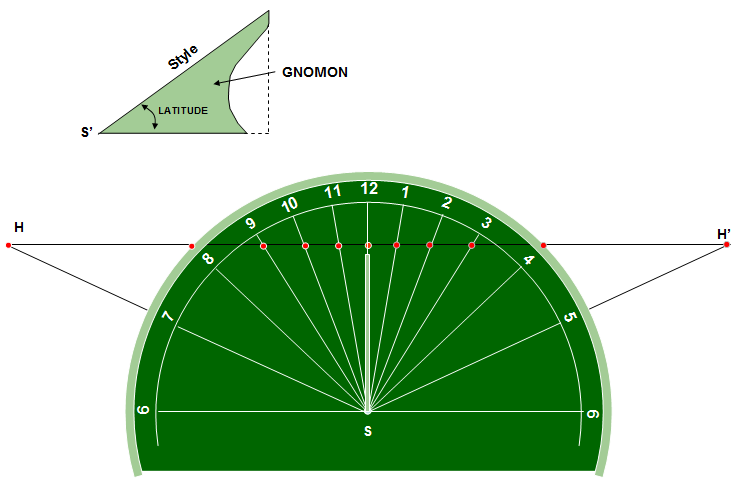
There you have it: It can be done with only compass and straight edge except for setting the latitude angle in Step 1. And once you have a drawing template for the sundial, you can make not only a dial for yourself, but one for your neighbor. In fact, it is most probable that Bannekar made templates for others to use. It would be wonderful if anyone finds one of these 250 year old drawings. Here is another dial using the construction lines, but this time using an octagonal outline with the point S set toward the bottom.