
Digital sundials have captured the imagination of many people, including cartoonists such as Wiley’s secret of Stonehenge shown below, which correctly displays the shadow bounds of the vertical stone gnomon. Two sundial enthusiasts who took Stewart’s article seriously were Robert Kellogg and Daniel Scharstein. Working independently, they both created and patented digital sundials that emulate Brother Benjamin’s mythic fractal sundial. Kellogg and Scharstein received nearly simultaneous patents, separated by only three weeks.
The first of these dials was developed by Kellogg in 1994, and described in a paper at the first North American Sundial Society’s (NASS) annual meeting on March 30, 1995 held at the Smithsonian Institution, Washington DC. The presentation was published in the September 1995 issue of NASS journal The Compendium, describing the digital dial as a “compound polar dial” (photo below left). By January 1997, the sundial was patented as USPTO 5,5,96,553 “Digital Sundial” with the leading illustration below center, and for a brief while commercially available shown in the photo below right
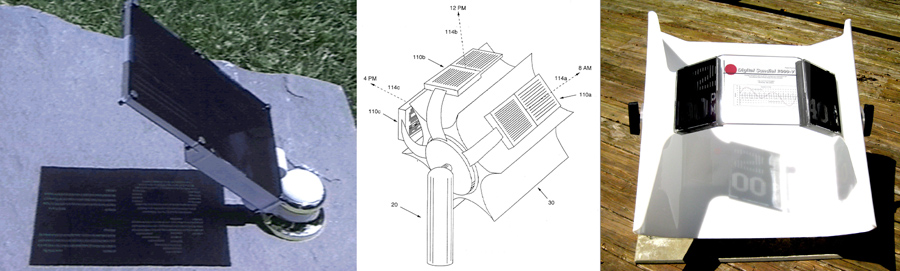
Kellogg’s Digital Dial [photo by permission of Bob Kellogg]
Meanwhile, Dan Scharstein, Hans Scharstein, and Werner Krotz-Vogel had the same idea for a digital dial and received a U.S. patent [Scharstein, Scharstein, and Krotz-Vogel, USPTO 5,590,093 December 31, 1996, “Digital Sundial”] three weeks earlier than Kellogg. In fact, Scharstein’s patent was submitted nearly six months before Kellogg, but in one of the irony’s of life, during the patent review process, Scharstein added Kellogg’s article as a reference from the September 1995 Compendium article. In any event Scharstein's digital sundial is quite elegant as shown in the phot below of patent drawing and an example of the sundial with Dan underneath.

Scharstein’s Digital Dial [photo by permission of Dan Scharstein]
The principle of operation of both Kellogg’s and Scharstein’s dial is nearly identical. Kellogg used a method of projecting sunlight and shadow onto a blank dial surface, much as Bizot, Thew, Brother Benjamin, and even Wiley. Scharstein added a translucent layer for immediate sunlight illumination such that the gnomon itself becomes the digital dial, much as Hine’s digital display or that of a modern digital clock. Scharstein’s has an elegant version of the digital dial for sale, as shown below. A mirror is used to view the numbers, making the dial both easier to read and avoiding the possibility of eye damage of directly seeing the sun.

Scharstein’s Dial Available for Purchase [photos by permission of Dan Scharstein]
The dial is nicely packaged and available at www.digitalsundial.com.
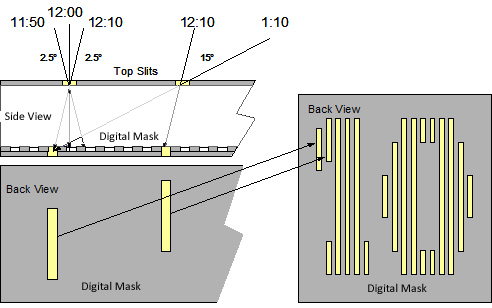
The underlying method of creating the digital numbers is common to both Kellogg’s and Scharstein’s dials. Two parallel layers are used, each containing vertical slits. A front layer allows a series of sunbeams to hit the second layer, and depending upon the angle of the sun, pass through a second series of slits. This second layer (or “digital mask”) contains interstitial slits that collectively illuminate as the time of day as illustrated below:
Although simple in conception, the art is in the construction, and requires the alignment of top and bottom surfaces to within 0.001” (25 micrometers). The photo at left shows a set of computer generated surfaces for one of Kellogg’s sundials. Note that the lower layer has numbers designed in reverse for projection onto a dial surface.
A closer look at the figure at left shows that the sunlight from the upper surface slit falls onto the lower digital mask through a refractive medium such as plexiglass. Then Snell's law of refraction must be used to determine where the exiting ray occurs.
Whether there is refraction or not, the distance that the sunlight beam moves is proportional to the tangent of the sun angle perpendicular to the surface of the dial. That is, the exact spacing of the digital mask slits is not uniform but must slightly increase if the dial is to keep exact solar time.
If the mask numbers are cyclically (that is, reused by the same slit overeveral hours), then the spacing cannot be made exact. Therefore, not only do Kellogg and Scharstein accommodate an error in the position of the digital slits, but both find a method to minimize the error. Actually, the problem of distributing errors such as these was first solved by the Russian mathematician Chebychev, who showed that a weighting factor could be applied to polynomials to redistribute the error. (As a side note, these weighting factors are used every day in the finite computations of sine, cosine and tangent functions performed on modern computers and hand-held calculators.)
