 In the late 1980’s and early 1990’s several interesting articles appeared in mathematical journals discussing the possibility of fractal and digital sundials. The works of Manfred Schroeder [1] and K.J. Falconer [2] describe Cantor-like fractals embedded in a higher dimension.
In the late 1980’s and early 1990’s several interesting articles appeared in mathematical journals discussing the possibility of fractal and digital sundials. The works of Manfred Schroeder [1] and K.J. Falconer [2] describe Cantor-like fractals embedded in a higher dimension.
Schroeder, in his article on “Fractals, Chaos, Power Laws” (1991) described a set of Venetian blinds: “[The ] idea underlying digital sundial is a set of bars that casts very different shadows depending on the direction of projection.”
Ultimately both Schroeder and Falconer imagined a multi-dimensional object, that when projected along one axis, casts a shadow, but when projected along another axis, shows only light with a “weightless” shadow. Although the mathematical principle is correct, the implementation is vague. As Schroeder stated, “...of course, the shadow-casting set is likely to be rather complicated, and the inventor understandably refrains from detailed instructions for its construction…”

[Andrew Christi - Scientific American, August 1991]
|
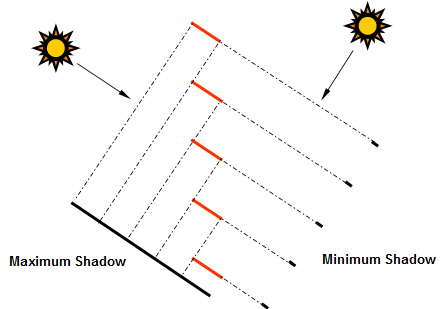
These ideas were summarized by Ian Stewart’s 1991 article on Mathematical Games in Scientific American [3], calling upon a mythical Brother Benjamin to describe the fractal dial, as shown in the figure at left. Stewart, unaware that a digital dial had already been invented, described the dial in terms of a complex set of Venetian Blinds. The fictitious abbot of the Cartesian Monastery understood that Venetian Blinds are able to pass sunlight for only a portion of a day.
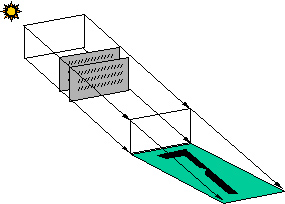
In each of the papers by Stewart, Schroeder, and Falconer, the illustration of the potential digital sundial is shown casting numerals far wider than the fractal gnomon. Although these illustrations certainly captured the minds of many sundial inventors, the true sundial numeral is confined within the shadow bounds of the gnomon, as illustrated below.
 1 Schroader, Manfred, “Fractals, Chaos, Power Laws - Minutes from an Infinite Paradise”, pp.181-183, W.H. Freeman and Company, New York, 1991.
1 Schroader, Manfred, “Fractals, Chaos, Power Laws - Minutes from an Infinite Paradise”, pp.181-183, W.H. Freeman and Company, New York, 1991.
2 Falconer, K.J., 1987, “Digital Sundials, Paradoxical Sets, and Vitushkin’s Conjecture”, The Mathematical Intelligencer, pp. 24-27, Vol. 9, No. 1, 1987.
3 Stewart, Ian, “What in Heaven is a Digital Sundial,” Scientific American, pp.104-106, August 1991.
