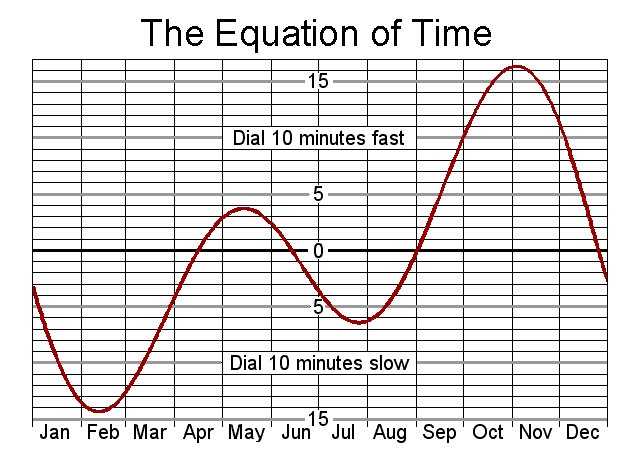
Even if your dial includes the longitude correction, its timekeeping will vary throughout the year due to a phenomenon called The Equation of Time. Simply put, the apparent motion of the sun compared to your watch will cause your dial to appear as much as 16 minutes" fast" or "slow" at various times of the year.
The Equation of Time is caused by the combination of two effects: (a) by the earth's elliptical orbit where the laws of Kepler tell the earth to speed faster near the sun than away...that is, at perihelion in December the earth's orbital change is faster that during the June aphelion, and (b) the 23.44° tilt of the earth's axis from the elciptic plane of its orbit.
The chart below shows the amount your dial will vary from clock time through the year. Right click on the graph, select save image for copy, and then print it out and keep it close to your dial. There are dials which compensate for the Equation of Time, but they are complicated.